RNN循环神经网络(一)
循环神经网络(RNN)是深度学习领域处理序列数据的基础架构,广泛应用于自然语言处理、语音识别、时间序列预测等任务。本文从零开始,深入剖析RNN的核心机制、参数共享原理以及前向传播过程,详细讲解梯度消失问题的数学本质,并系统介绍LSTM如何通过门控机制有效解决长距离依赖。此外,还将探讨双向RNN、深度RNN、GRU等高级架构变体的设计思想与实际应用场景,帮助读者全面掌握RNN及其演进历程。
1. 为什么需要序列模型?
1.1 传统神经网络的局限
传统的神经网络(如多层感知机 MLP)假设输入和输出是相互独立的,但在处理文本、语音或时间序列数据时,这个假设并不成立。序列数据具有两个关键特征,使得传统神经网络难以处理:
1.2 序列模型的核心特征
顺序依赖性(Sequential Dependency)
输入元素的顺序对最终的语义至关重要。例如:
- “我不喜欢吃饭” vs “我喜欢不吃饭” - 虽然包含相同的字,但由于顺序不同,意义完全不同
- “张三打了李四” vs “李四打了张三” - 主语和宾语的位置决定了动作的方向
可变长度(Variable Length)
输入和输出的长度往往不固定且相互独立:
- 机器翻译:英文 “How are you?” (3个词) → 中文 “你好吗?” (3个字)
- 情感分析:任意长度的评论 → 单个情感标签(正面/负面)
- 文本生成:一个主题词 → 完整的段落或文章
1.3 典型应用场景
| 应用领域 | 输入 | 输出 | 示例 |
|---|---|---|---|
| 语音识别 | 音频波形序列 | 文本序列 | 语音 → “今天天气不错” |
| 情感分析 | 文本序列 | 分类标签 | “这部电影太棒了” → 正面 |
| 机器翻译 | 源语言序列 | 目标语言序列 | “Hello” → “你好” |
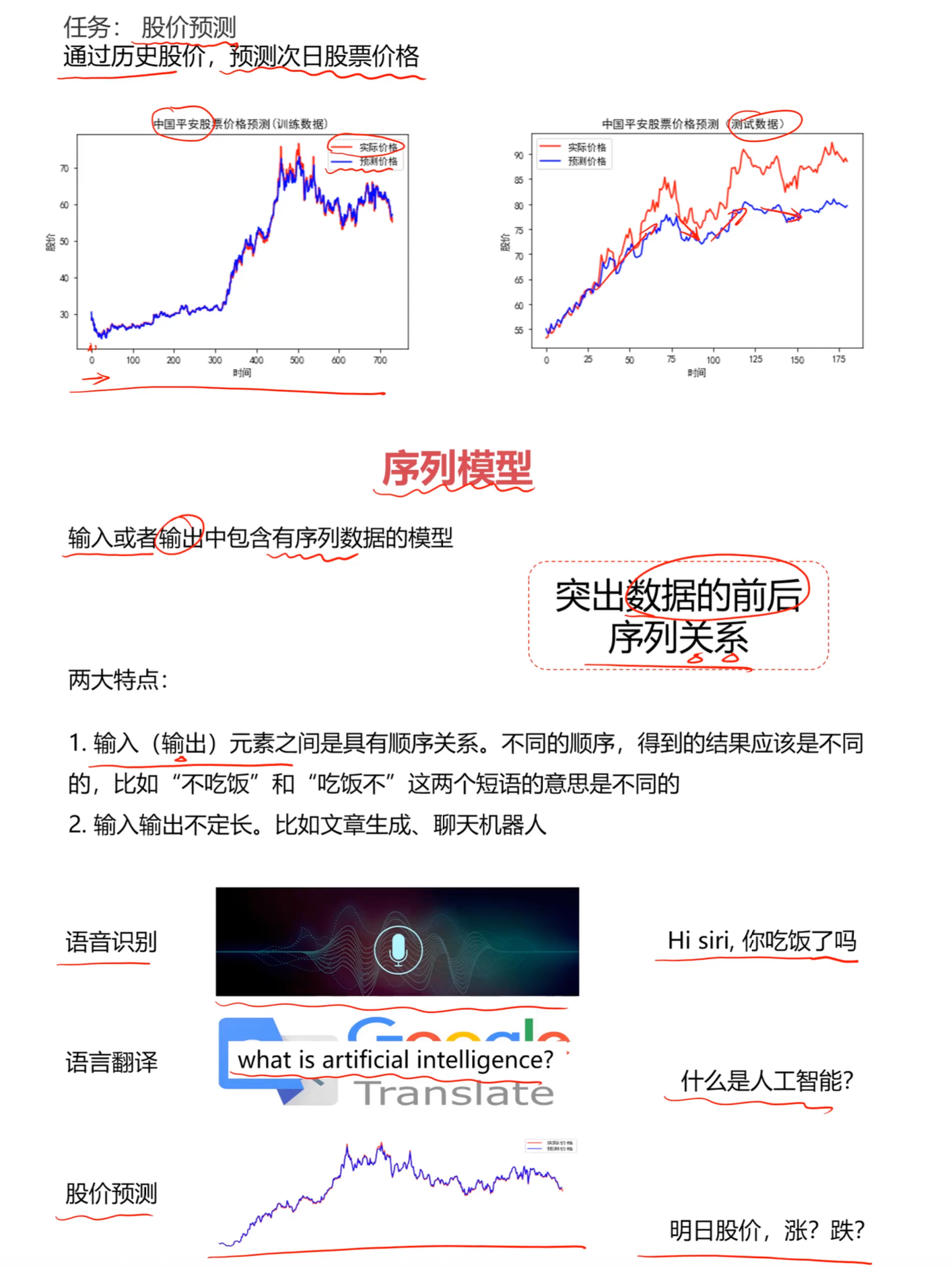
| 股票预测 | 历史价格序列 | 未来价格 | [p1, p2, …, pn] → pn+1 |
| 命名实体识别 | 文本序列 | 标注序列 | “马云在杭州” → [人名, 介词, 地名] |
2. 文本数据的数值化表示
2.1 为什么需要数值化?
计算机只能处理数字,因此需要将文本转换为数值表示。这个过程称为词向量化(Word Embedding)或编码(Encoding)。
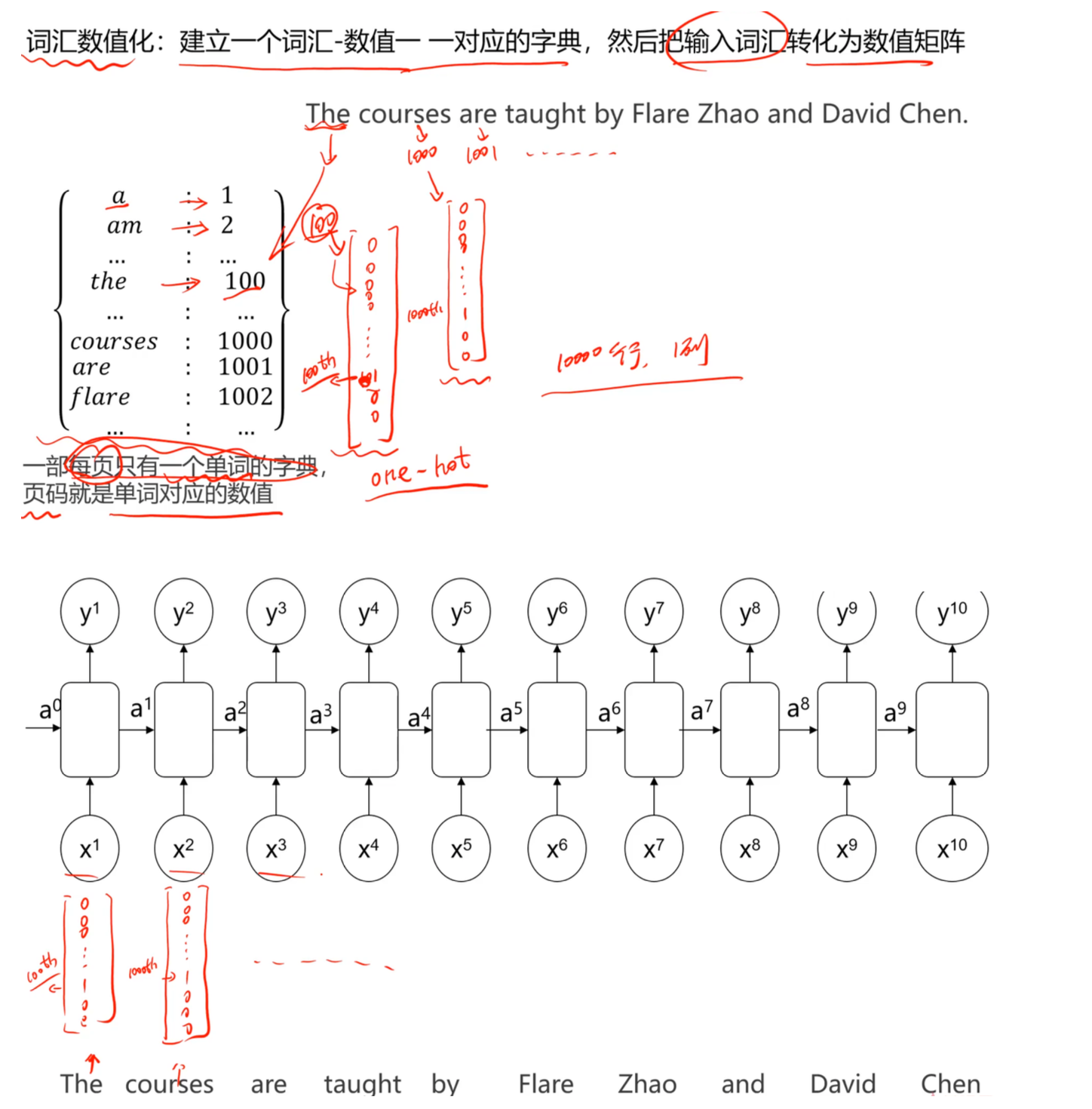
2.2 字典映射(Dictionary Mapping)
基本原理
建立一个包含所有可能词汇的字典(词汇表),为每个词分配唯一的整数索引。
示例
vocabulary = {
"hello": 0,
"world": 1,
"deep": 2,
"learning": 3,
"is": 4,
"awesome": 5
}
sentence = "deep learning is awesome"
encoded = [2, 3, 4, 5] # 转换为索引序列
2.3 One-Hot编码
原理说明
将每个词表示为一个高维稀疏向量。假设词汇表大小为 $V$ ,则每个词是一个长度为 $V$ 的向量,只在对应位置为1,其余位置为0。
数学表示
对于词汇表大小 $V=10000$,如果 “learning” 的索引是 3:
learning = [0, 0, 0, 1, 0, 0, ..., 0] # 第3位为1,其余为0
↑______________________↑
位置0 位置9999
完整流程
- 分词:将句子拆分为单词
- 建立词典:统计所有唯一词汇,建立映射关系
- 编码:将每个词转换为One-Hot向量
- 序列输入:将向量序列 $[x^{1}, x^{2}, …, x^{T}]$ 送入模型
局限性
- 维度过高(通常10,000-100,000维)
- 无法表达词与词之间的语义相似性
- 存储和计算效率低
改进方案:使用词嵌入(Word Embedding),如Word2Vec、GloVe,将词映射到低维稠密向量空间(通常100-300维)。
3. RNN的核心机制
3.1 什么是"记忆"?
RNN的本质是带记忆的神经网络。与传统神经网络不同,RNN通过隐藏状态(Hidden State) $h^{(t)}$ 将历史信息传递到未来时间步。
3.2 前向传播过程
在时间步 $t$,RNN接收两个输入:
- 当前输入 $x^{(t)}$:当前时刻的数据(如当前单词)
- 历史状态 $h^{(t-1)}$:上一时刻的隐藏状态(包含历史信息)
计算公式
$$ \begin{align} h^{(t)} &= \tanh(W_{hh} h^{(t-1)} + W_{xh} x^{(t)} + b_h) \\ y^{(t)} &= \text{softmax}(W_{hy} h^{(t)} + b_y) \end{align} $$
其中:
- $W_{hh}$:隐藏层到隐藏层的权重矩阵(记忆传递)
- $W_{xh}$:输入层到隐藏层的权重矩阵(当前输入)
- $W_{hy}$:隐藏层到输出层的权重矩阵(生成输出)
- $b_h, b_y$:偏置项
- $\tanh$:激活函数,将值压缩到 $[-1, 1]$ 范围
- $\text{softmax}$:用于多分类任务的输出层
3.3 参数共享机制
关键特性:所有时间步共享相同的权重参数 $W_{hh}, W_{xh}, W_{hy}$
优势:
- 参数数量固定:与序列长度无关,避免参数爆炸
- 泛化能力强:学到的模式可应用于不同位置
- 计算效率高:减少训练参数
示例
处理句子 “I love deep learning” 时:
# 伪代码
h0 = zeros(hidden_size) # 初始隐藏状态
h1 = tanh(Whh @ h0 + Wxh @ x1 + bh) # 处理 "I"
h2 = tanh(Whh @ h1 + Wxh @ x2 + bh) # 处理 "love"(使用相同的Whh和Wxh)
h3 = tanh(Whh @ h2 + Wxh @ x3 + bh) # 处理 "deep"
h4 = tanh(Whh @ h3 + Wxh @ x4 + bh) # 处理 "learning"
3.4 损失函数与训练
单步损失
对于时间步 $t$,如果真实标签是 $\hat{y}^{(t)}$,预测值是 $y^{(t)}$,则:
$$ \mathcal{L}^{(t)} = -\sum_{k} \hat{y}_k^{(t)} \log(y_k^{(t)}) $$ (交叉熵损失,用于分类任务)
总体损失
整个序列的损失是所有时间步损失的累加: $$ \mathcal{L} = \sum_{t=1}^{T} \mathcal{L}^{(t)} $$
反向传播
RNN使用时间反向传播算法(BPTT, Backpropagation Through Time):
- 从最后时间步开始,向前计算梯度
- 梯度沿着时间轴反向流动
- 累积所有时间步的梯度更新参数
4. RNN的四种架构
根据输入序列长度 $T_x$ 和输出序列长度 $T_y$ 的关系,RNN有四种典型架构:
4.1 多对多(同步,$T_x = T_y$)
结构特点
每个输入时间步对应一个输出时间步。
应用场景
- 命名实体识别(NER):识别句子中的人名、地名
输入: "张三在北京工作"
输出: [人名, 介词, 地名, 动词]
- 词性标注(POS Tagging)
- 视频帧标注:为每一帧打标签
网络结构图
x1 → [RNN] → y1
↓
x2 → [RNN] → y2
↓
x3 → [RNN] → y3
4.2 多对一($T_x > 1, T_y = 1$)
结构特点
整个输入序列产生一个输出。
应用场景
- 情感分析
输入: "这部电影的剧情很精彩,演员表现也很出色"
输出: 正面(1个标签)
- 文本分类:新闻分类、垃圾邮件检测
- 序列异常检测
网络结构图
x1 → [RNN]
↓
x2 → [RNN]
↓
x3 → [RNN] → y(只在最后输出)
4.3 一对多($T_x = 1, T_y > 1$)
结构特点
一个输入产生多个输出。
应用场景
- 音乐生成:给定一个音符,生成完整旋律
- 图像描述生成:一张图片 → 描述句子
输入: [猫的图片]
输出: "一只橘猫坐在窗台上"(多个词)
- 故事/诗歌创作:给定主题词,生成完整内容
网络结构图
x → [RNN] → y1
↓
[RNN] → y2
↓
[RNN] → y3
4.4 多对多(异步,$T_x \neq T_y$)
结构特点
输入和输出序列长度不同,通常先编码再解码。
应用场景
- 机器翻译
输入(英文3词): "How are you"
输出(中文5字): "你好吗朋友"
- 对话系统:问题 → 回答
- 文本摘要:长文本 → 简短摘要
网络结构(Encoder-Decoder)
编码器阶段:
x1 → [RNN]
↓
x2 → [RNN]
↓
x3 → [RNN] → 上下文向量 c
解码器阶段:
c → [RNN] → y1
↓
[RNN] → y2
↓
[RNN] → y3
↓
[RNN] → y4
↓
[RNN] → y5
5. RNN的致命缺陷:梯度消失问题
5.1 问题描述
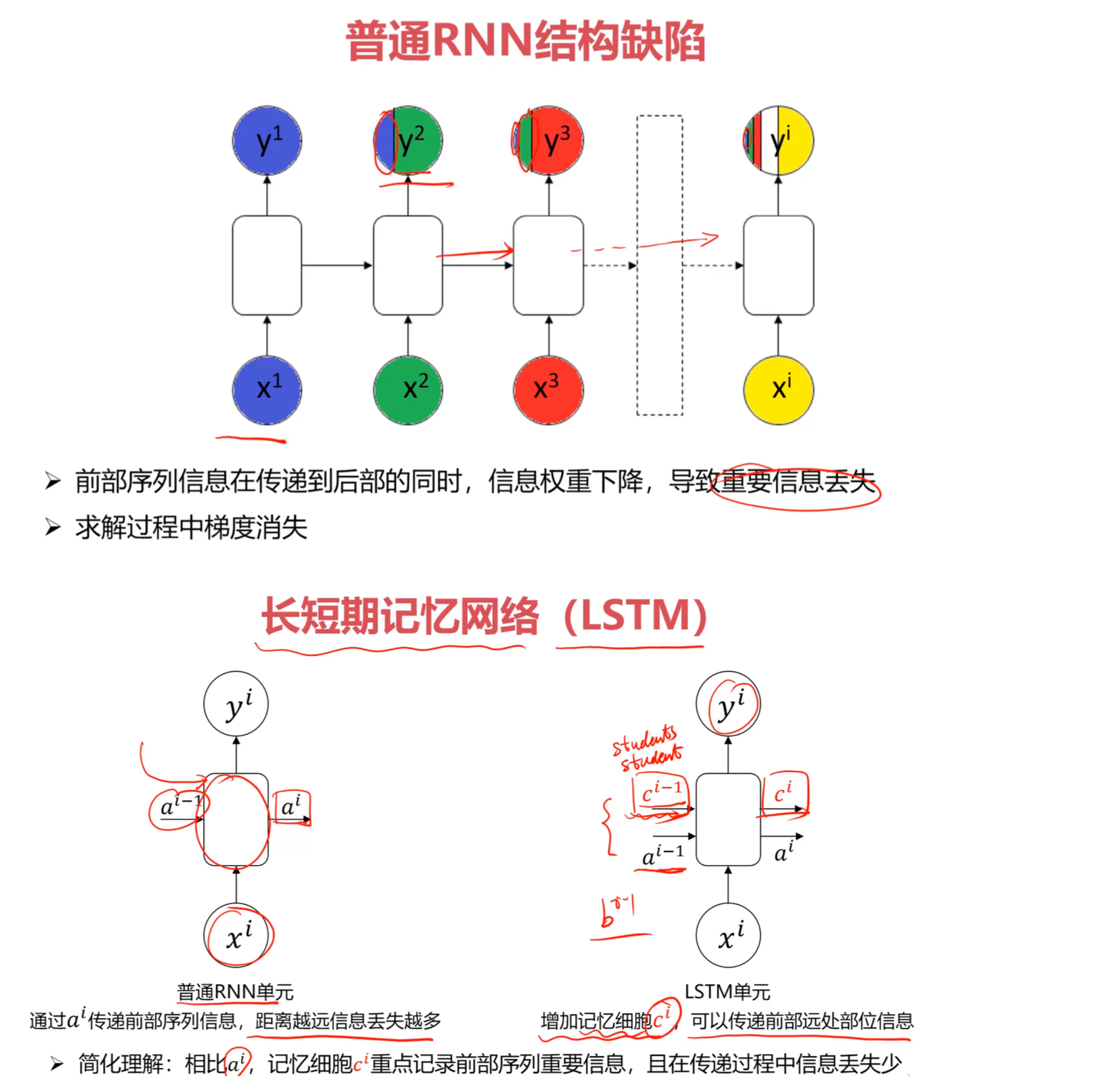
普通RNN在处理长序列时存在严重的 梯度消失(Vanishing Gradient) 问题:
现象:前面时间步的信息在传递到后面时逐渐衰减,导致长距离依赖关系无法学习。
数学原因
在反向传播时,梯度需要连乘多个 $W_{hh}$: $$ \frac{\partial \mathcal{L}}{\partial h^{(1)}} = \frac{\partial \mathcal{L}}{\partial h^{(T)}} \cdot \prod_{t=2}^{T} \frac{\partial h^{(t)}}{\partial h^{(t-1)}} $$
如果 $\frac{\partial h^{(t)}}{\partial h^{(t-1)}} < 1$(通常由于激活函数导数 $< 1$),连乘后梯度趋近于0。
5.2 实际案例
语法一致性问题
考虑以下两个句子:
句子A: The cat, which ate the fish yesterday, was hungry.
句子B: The cats, which ate the fish yesterday, were hungry.
模型需要:
- 记住开头的主语是单数(cat)还是复数(cats)
- 在很多词之后,正确预测动词形式(was/were)
问题:如果中间插入的内容很长(如20-30个词),普通RNN会"忘记"主语的单复数信息,导致预测错误。
5.3 梯度爆炸问题
与梯度消失相反,如果 $\frac{\partial h^{(t)}}{\partial h^{(t-1)}} > 1$,连乘后梯度会指数级增长,导致梯度爆炸(Exploding Gradient)。
解决方案:梯度裁剪(Gradient Clipping)
if gradient.norm() > threshold:
gradient = gradient * (threshold / gradient.norm())
6. LSTM:长短期记忆网络
6.1 核心思想
LSTM(Long Short-Term Memory)通过引入记忆细胞(Memory Cell) $c^{(t)}$ 和门控机制(Gate Mechanism),解决了长距离依赖问题。
关键对比
| 特性 | 普通RNN | LSTM |
|---|---|---|
| 状态变量 | 隐藏状态 $h$ | 隐藏状态 $h$ + 记忆细胞 $c$ |
| 信息传递 | 直接传递,容易衰减 | 通过"传送带"机制,信息保持能力强 |
| 长距离依赖 | 难以学习(梯度消失) | 可以有效学习 |
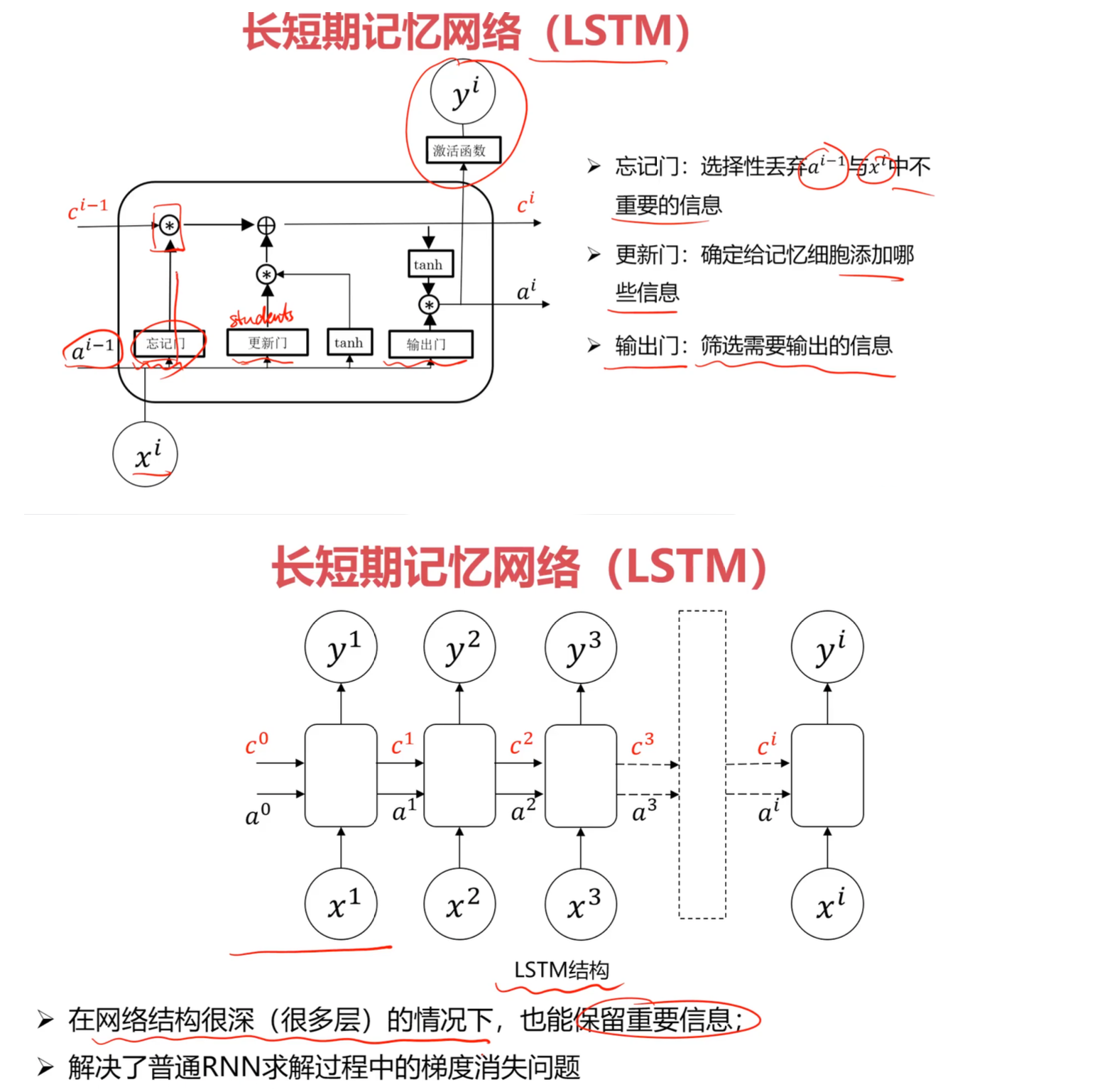
6.2 LSTM的三个门
LSTM通过三个门来精确控制信息的流动:
1. 遗忘门(Forget Gate)
功能:决定从记忆细胞中丢弃哪些信息
$$ f^{(t)} = \sigma(W_f \cdot [h^{(t-1)}, x^{(t)}] + b_f) $$
其中 $\sigma$ 是sigmoid函数,输出范围 $[0, 1]$:
- $f^{(t)} = 0$:完全遗忘
- $f^{(t)} = 1$:完全保留
示例:当遇到新主语时,遗忘旧主语的单复数信息。
2. 输入门(Input Gate)
功能:决定将哪些新信息存储到记忆细胞
$$ \begin{align} i^{(t)} &= \sigma(W_i \cdot [h^{(t-1)}, x^{(t)}] + b_i) \\ \tilde{c}^{(t)} &= \tanh(W_c \cdot [h^{(t-1)}, x^{(t)}] + b_c) \end{align} $$
- $i^{(t)}$:输入门控信号(0-1之间)
- $\tilde{c}^{(t)}$:候选值(新信息内容)
示例:记录新主语是单数还是复数。
3. 输出门(Output Gate)
功能:决定从记忆细胞中输出什么信息
$$ \begin{align} o^{(t)} &= \sigma(W_o \cdot [h^{(t-1)}, x^{(t)}] + b_o) \\ h^{(t)} &= o^{(t)} \cdot \tanh(c^{(t)}) \end{align} $$
示例:根据记忆的主语信息,决定输出 “was” 还是 “were”。
6.3 记忆细胞更新
完整更新过程 $$ c^{(t)} = f^{(t)} \odot c^{(t-1)} + i^{(t)} \odot \tilde{c}^{(t)} $$
其中 $\odot$ 表示逐元素乘法(element-wise multiplication)。
直观理解
新记忆 = (遗忘门 × 旧记忆) + (输入门 × 新信息)
传送带比喻
记忆细胞 $c$ 就像一条传送带:
- 信息可以沿着传送带不受阻碍地传递(避免梯度消失)
- 门控机制可以精确地向传送带添加或移除信息
- 这种机制使得信息可以跨越很多时间步保持不变
6.4 LSTM的优势
- 缓解梯度消失:记忆细胞的加法更新(而非乘法)保持梯度流动
- 选择性记忆:通过门控机制学习什么信息重要、什么可以遗忘
- 长距离依赖:可以有效处理100+时间步的长序列
实验对比
| 任务类型 | 普通RNN准确率 | LSTM准确率 |
|---|---|---|
| 短序列(<10步) | 85% | 87% |
| 中序列(10-30步) | 65% | 82% |
| 长序列(>50步) | 40% | 78% |
7. 高级架构变体
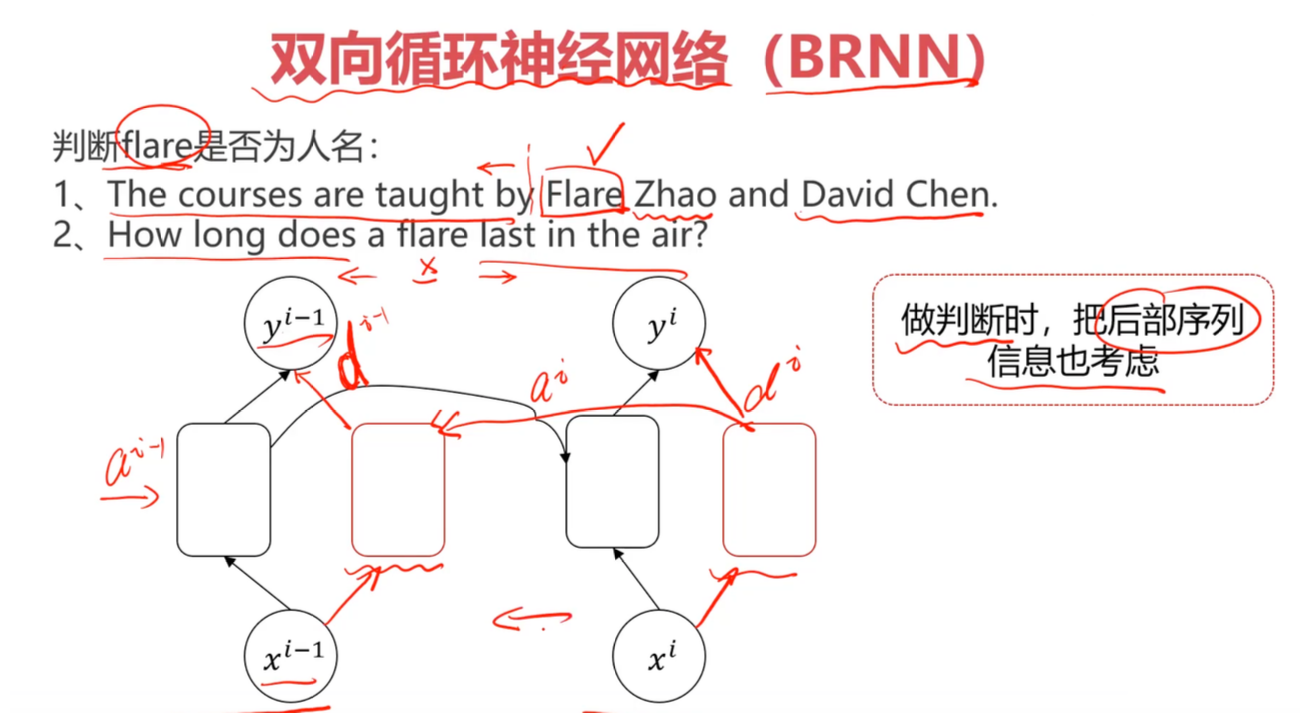
7.1 双向RNN(Bidirectional RNN, BRNN)
动机
单向RNN只能利用历史信息,无法看到未来。但在某些任务中,上下文信息都很重要。
典型案例
判断 “The courses are taught by Flare Zhao” 中 “Flare” 是否为人名:
- 仅看前文 “The courses are taught by”:无法确定
- 看到后文 “Zhao”(典型姓氏):可以确认 “Flare Zhao” 是人名
架构设计
同时训练两个RNN:
- 前向RNN(Forward):从左到右读取序列
- 后向RNN(Backward):从右到左读取序列
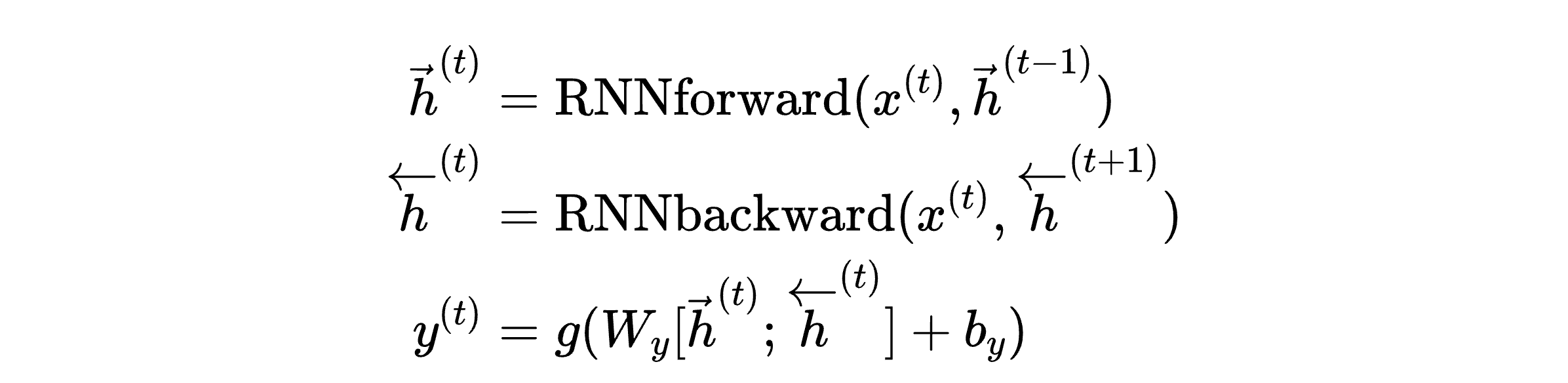
应用场景
- 命名实体识别(NER)
- 词性标注(POS Tagging)
- 填空题(完形填空)
局限性
- 计算成本翻倍
- 不适用于实时任务(需要等待完整序列)
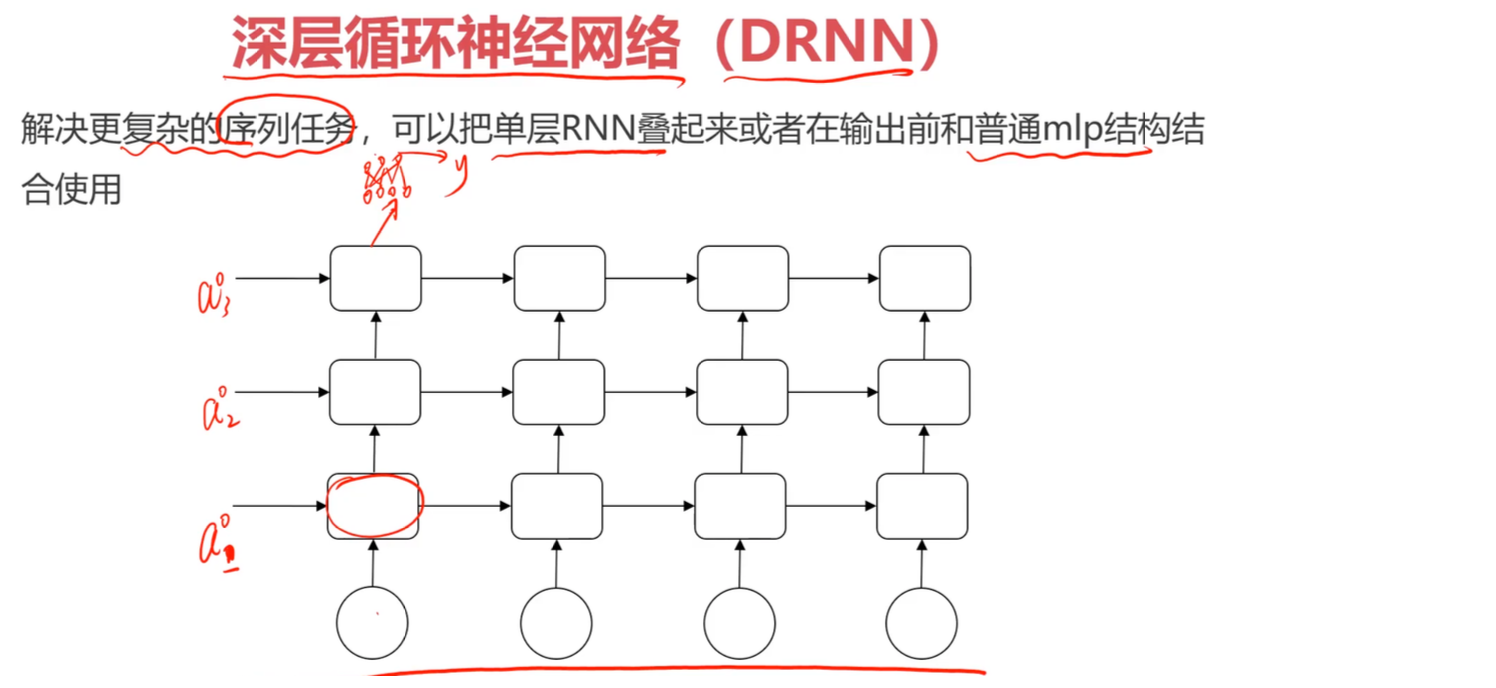
7.2 深度RNN(Deep RNN, DRNN)
动机
增加网络深度以学习更复杂的表示。
架构设计
垂直堆叠多个RNN层:
第3层: h1(3) → h2(3) → h3(3) → ... → output
↑ ↑ ↑
第2层: h1(2) → h2(2) → h3(2) → ...
↑ ↑ ↑
第1层: h1(1) → h2(1) → h3(1) → ...
↑ ↑ ↑
输入: x1 x2 x3
更新公式
对于第 $l$ 层: $$ h^{(t)[l]} = g(W^{[l]} h^{(t)[l-1]} + U^{[l]} h^{(t-1)[l]} + b^{[l]}) $$
实践建议
- 通常2-4层即可(过深容易过拟合)
- 可以在最后添加全连接层进行最终预测
- 使用残差连接(Residual Connection)缓解梯度消失
7.3 GRU(门控循环单元)
简化版的LSTM
GRU(Gated Recurrent Unit)将LSTM的三个门简化为两个:
- 更新门(Update Gate):结合了遗忘门和输入门
- 重置门(Reset Gate):控制前一时刻信息的使用程度
优势
- 参数更少(训练更快)
- 性能与LSTM相当
何时使用GRU
- 数据量较小
- 计算资源有限
- 需要快速实验
8. 实践建议与最佳实践
8.1 选择合适的架构
| 任务类型 | 推荐架构 | 理由 |
|---|---|---|
| 情感分类 | 多对一 LSTM/GRU | 需要整体语义理解 |
| 机器翻译 | 多对多(Encoder-Decoder)+ 注意力 | 长度不一致且需要对齐 |
| 命名实体识别 | 双向LSTM + CRF | 需要上下文信息 |
| 文本生成 | 一对多 LSTM + Attention | 需要长程依赖 |
8.2 超参数调优
关键超参数
- 隐藏层大小:128-512(视任务复杂度)
- 层数:1-3层(过深易过拟合)
- 学习率:0.001-0.01(使用Adam优化器)
- Dropout:0.2-0.5(防止过拟合)
- 梯度裁剪阈值:5-10
8.3 常见问题与解决方案
问题1:训练速度慢
- 使用GRU代替LSTM
- 减少序列长度(截断或采样)
- 使用更小的batch size
- 考虑使用Transformer架构(并行计算)
问题2:过拟合
- 增加Dropout比例
- 使用L2正则化
- 数据增强(同义词替换、回译等)
- 早停(Early Stopping)
问题3:梯度消失仍然存在
- 使用残差连接(Residual Connection)
- 尝试Layer Normalization
- 减少序列长度
- 使用注意力机制(Attention)
9. 总结与展望
9.1 核心要点回顾
- RNN的本质:通过隐藏状态传递信息,处理序列数据
- 参数共享:所有时间步使用相同权重,提高泛化能力
- 梯度消失:普通RNN的致命缺陷,限制长距离依赖学习
- LSTM/GRU:通过门控机制有效缓解梯度消失
- 架构选择:根据输入输出关系选择合适的RNN类型
9.2 RNN的局限性
尽管LSTM/GRU改进了普通RNN,但仍存在问题:
- 顺序计算:无法并行化,训练速度慢
- 长序列仍有瓶颈:100步以上效果下降
- 上下文向量瓶颈:Encoder-Decoder结构中,整个输入需压缩到固定维度
9.3 现代替代方案
Transformer(2017年提出)已在大多数NLP任务中取代RNN:
- 并行计算:通过自注意力机制实现
- 长距离依赖:直接建模任意位置间的关系
- 可扩展性:支持超大规模预训练(GPT、BERT等)
何时仍使用RNN
- 实时流式任务(语音识别)
- 资源受限场景(边缘设备)
- 时间序列预测(股票、传感器数据)
10. 其他参考资料
经典论文
- Hochreiter & Schmidhuber (1997): “Long Short-Term Memory” - LSTM原始论文
- Cho et al. (2014): “Learning Phrase Representations using RNN Encoder-Decoder” - GRU提出
- Vaswani et al. (2017): “Attention is All You Need” - Transformer架构
实践教程
开源项目
- Karpathy的char-rnn - 经典的字符级RNN
- Fairseq - Facebook的序列建模工具库