加速光线追踪算法优化

发表于： 2023-02-22 分类于：计算机图形学

字数： 1051 阅读：≈ 5分钟

在上一篇文章中，我们学习了光线追踪的基本原理：向场景发射光线，并计算它与物体是否相交。听起来很简单，对吧？

但这里隐藏着一个巨大的性能陷阱：假设你的场景中有 1000 万个三角形，需要渲染 1920×1080 分辨率的图像。

朴素做法：每条光线都与这 1000 万个三角形逐一进行求交测试
时间复杂度：O(像素数 × 三角形数) ≈ 2M × 10M = 20 万亿次计算
实际后果：渲染一帧可能需要几天甚至几周

本文基于 GAMES101 Lecture 14 的内容，介绍三种主流的光线追踪加速结构，帮助你理解现代渲染器如何将渲染时间从几天缩短到几秒。

核心思想：如果光线连物体所在的区域都没碰到，那就不需要测试区域内的物体。

一、均匀网格（Uniform Grids）

1.1 基本思想

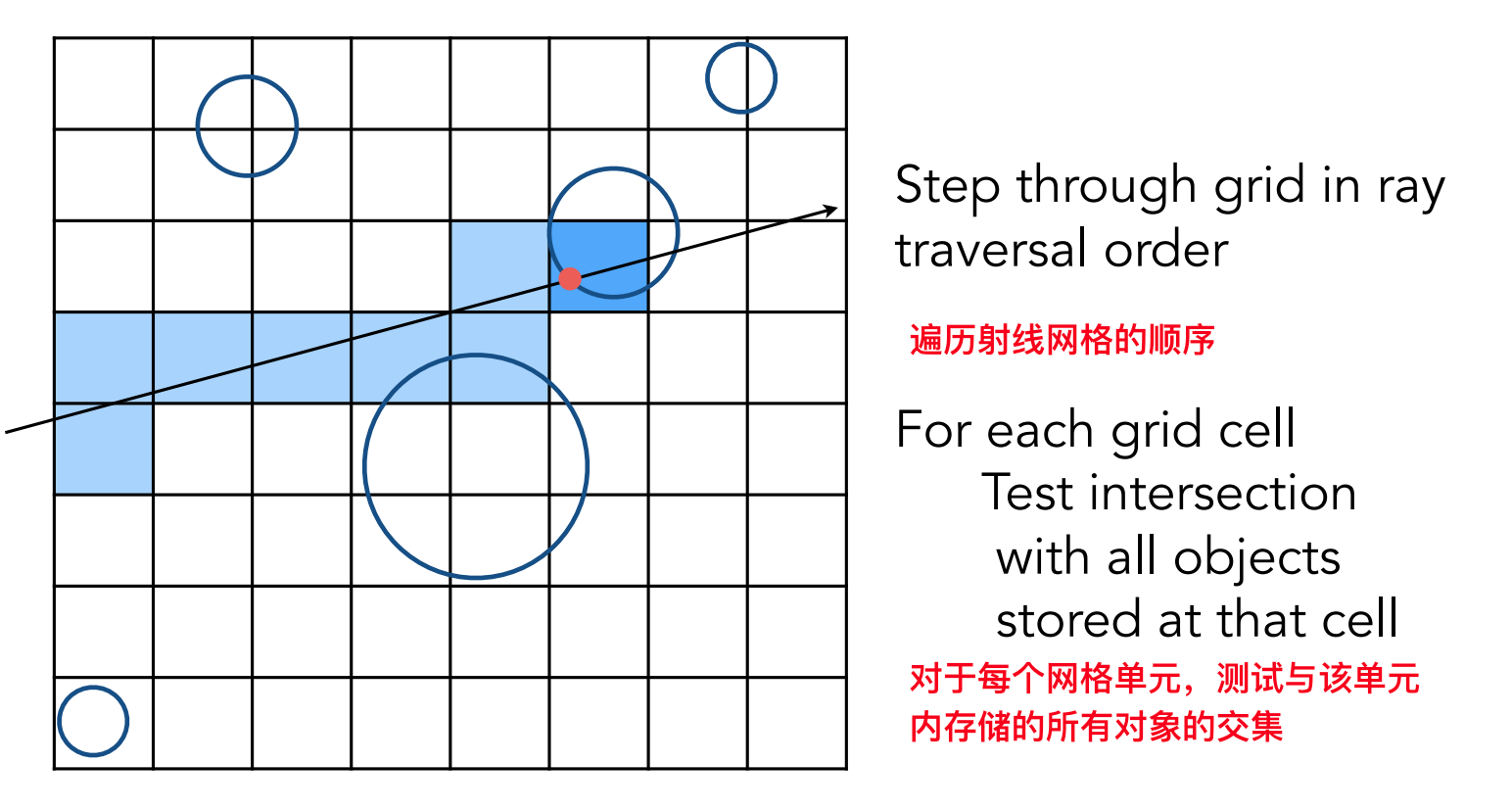
将整个场景像切蛋糕一样，划分成大小均匀的网格（Voxels），每个格子记录其中包含的物体。

1.2 工作流程

预处理阶段：

计算包围整个场景的轴对齐包围盒（AABB）
将包围盒均匀划分为 nx × ny × nz 个网格单元
遍历所有物体，将其注册到与之相交的所有网格中

光线遍历阶段：

光线从起点开始，按照 3D-DDA 算法逐格前进
每进入一个网格，检查该格是否包含物体
如果包含，则与格内所有物体进行精确求交测试
找到最近交点后终止遍历

def traverse_grid(ray, grid):
    """3D-DDA 光线网格遍历"""
    current_cell = get_entry_cell(ray)

    while current_cell in grid:
        if grid[current_cell].has_objects():
            hit = intersect_objects(ray, grid[current_cell].objects)
            if hit:
                return hit

        current_cell = next_cell(ray, current_cell)  # 移动到下一个格子

    return None

1.3 优缺点分析

优点：

实现简单，易于理解
当物体均匀分布时（如粒子系统、体积数据），性能优秀
网格访问为 O(1)，空间划分规则

缺点：

“体育场里的茶壶”（Teapot in a Stadium）问题
- 场景：巨大的空旷体育场中心放一个小茶壶
- 困境：为了精细表示茶壶需要细分网格 → 光线要遍历成千上万个空格子 → 性能崩溃
- 根本原因：无法适应物体分布不均匀的场景

二、空间划分：KD-Tree

2.1 设计动机

为了解决均匀网格的"体育场茶壶"问题，自适应空间划分方法应运而生：

核心思想：根据物体密度动态调整空间划分粒度
策略：物体密集区域细分，空旷区域保持大块

2.2 KD-Tree 原理

KD-Tree（K-Dimensional Tree）是一种二叉空间划分树：

构建过程：

选择一个坐标轴（x/y/z 循环选择）和分割位置
沿该轴将空间一分为二
对左右子空间递归执行 1-2 步
当节点内物体数量 ≤ 阈值时停止分割

节点结构：

class KDNode:
    # 内部节点
    axis: int          # 分割轴 (0=x, 1=y, 2=z)
    split_pos: float   # 分割位置
    left: KDNode       # 左子树
    right: KDNode      # 右子树

    # 叶子节点
    objects: List      # 物体列表

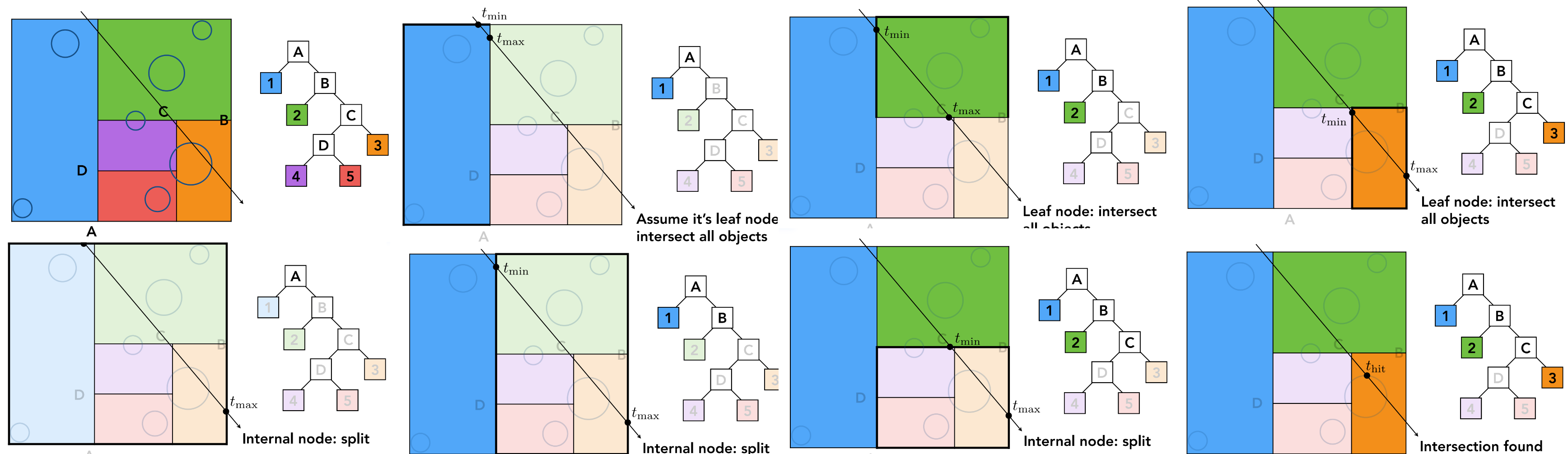
2.3 光线遍历算法

def traverse_kdtree(ray, node):
    """递归遍历 KD-Tree"""
    if node.is_leaf():
        return intersect_objects(ray, node.objects)

    # 判断光线在分割平面的哪一侧
    if ray.origin[node.axis] < node.split_pos:
        near, far = node.left, node.right
    else:
        near, far = node.right, node.left

    # 先查近端
    hit = traverse_kdtree(ray, near)
    if hit:
        return hit

    # 如果光线穿过分割平面，查远端
    if ray_crosses_split_plane(ray, node):
        return traverse_kdtree(ray, far)

    return None

2.4 致命缺陷

物体重复存储问题：虽然 KD-Tree 很好地解决了空间分布不均的问题，但它有两个明显的缺点，导致现代光线追踪（尤其是动态场景）较少使用它。构建困难：很难确定一个完美的划分位置，且一旦物体移动（动态场景），整棵树很难高效更新。

后果：

内存占用增加（最坏情况指数级膨胀）
同一物体可能被多次求交
维护复杂度高

现状：由于这个缺陷，KD-Tree 在光线追踪领域已被 BVH 取代。

三、物体划分：BVH（工业界首选）

3.1 设计思想的根本转变

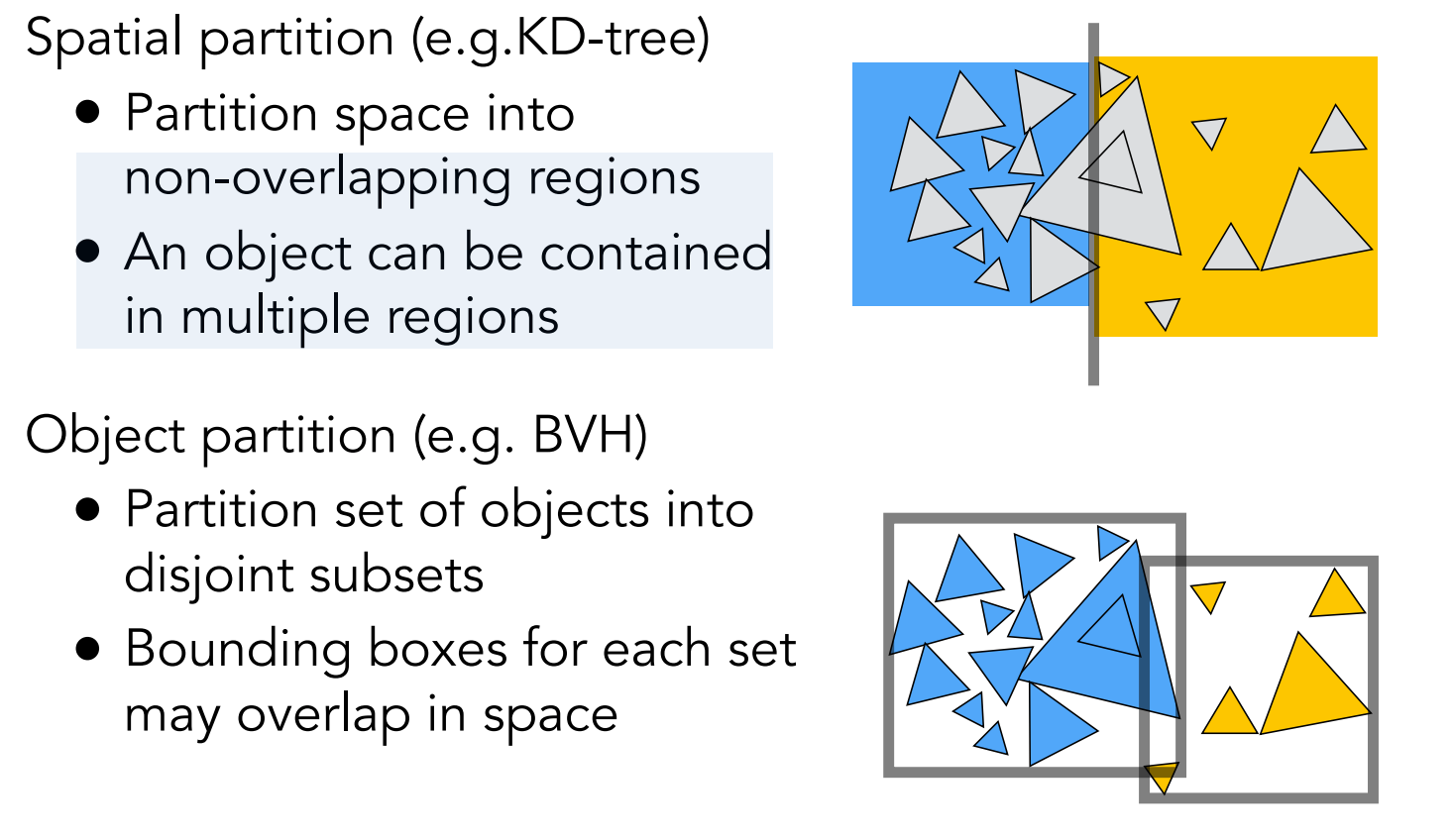
为了解决 KD-Tree 的物体重复存储问题，BVH（Bounding Volume Hierarchy，层次包围盒）采用了完全不同的策略：

维度	KD-Tree	BVH
划分对象	空间	物体
策略	沿坐标轴切割空间	将物体分组打包
节点内容	空间区域	物体集合的包围盒
物体归属	可能属于多个节点	仅属于一个节点
包围盒关系	严格不相交	可能重叠

核心优势：每个物体只出现在一个叶子节点中，彻底避免了重复存储。

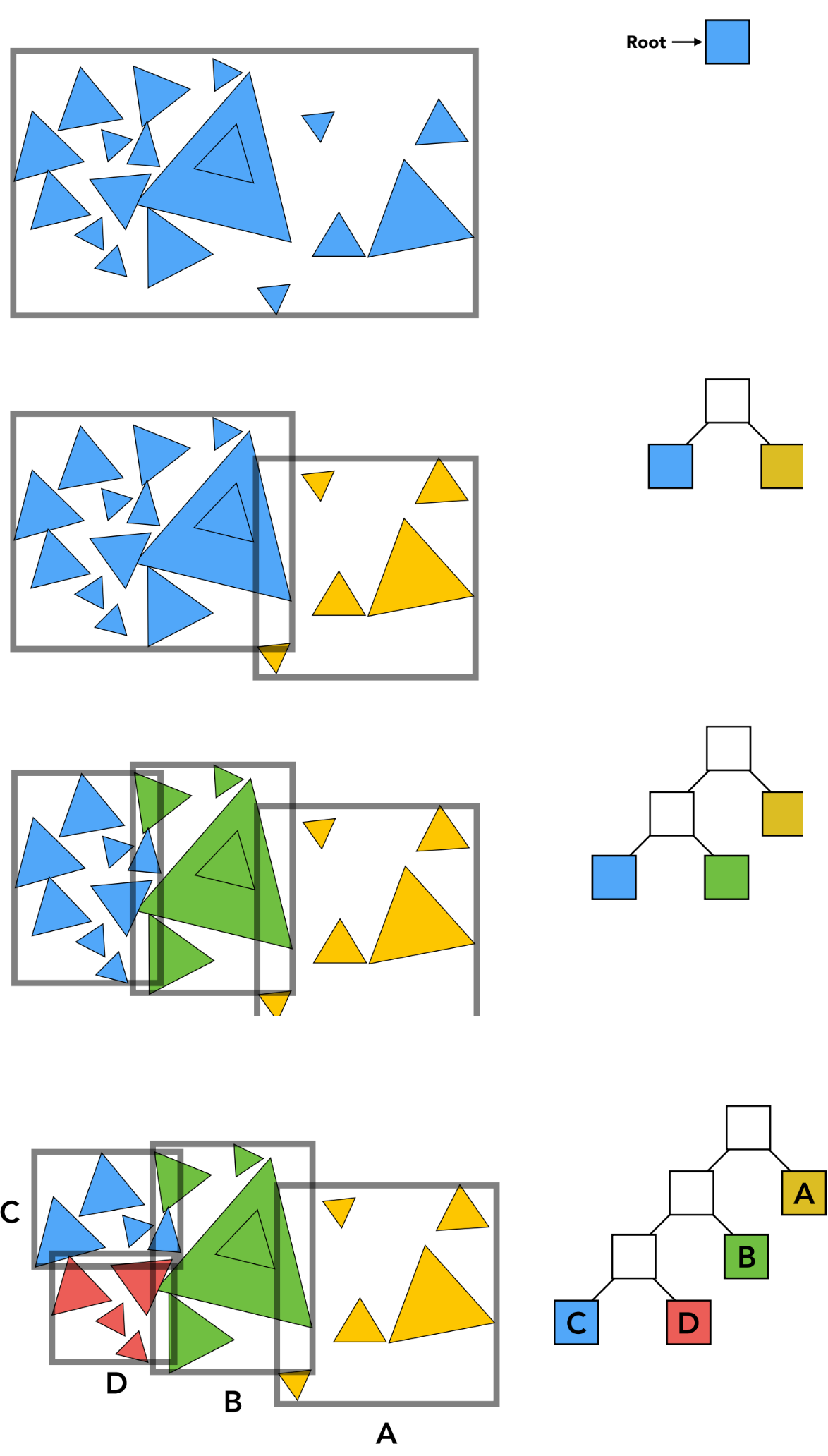
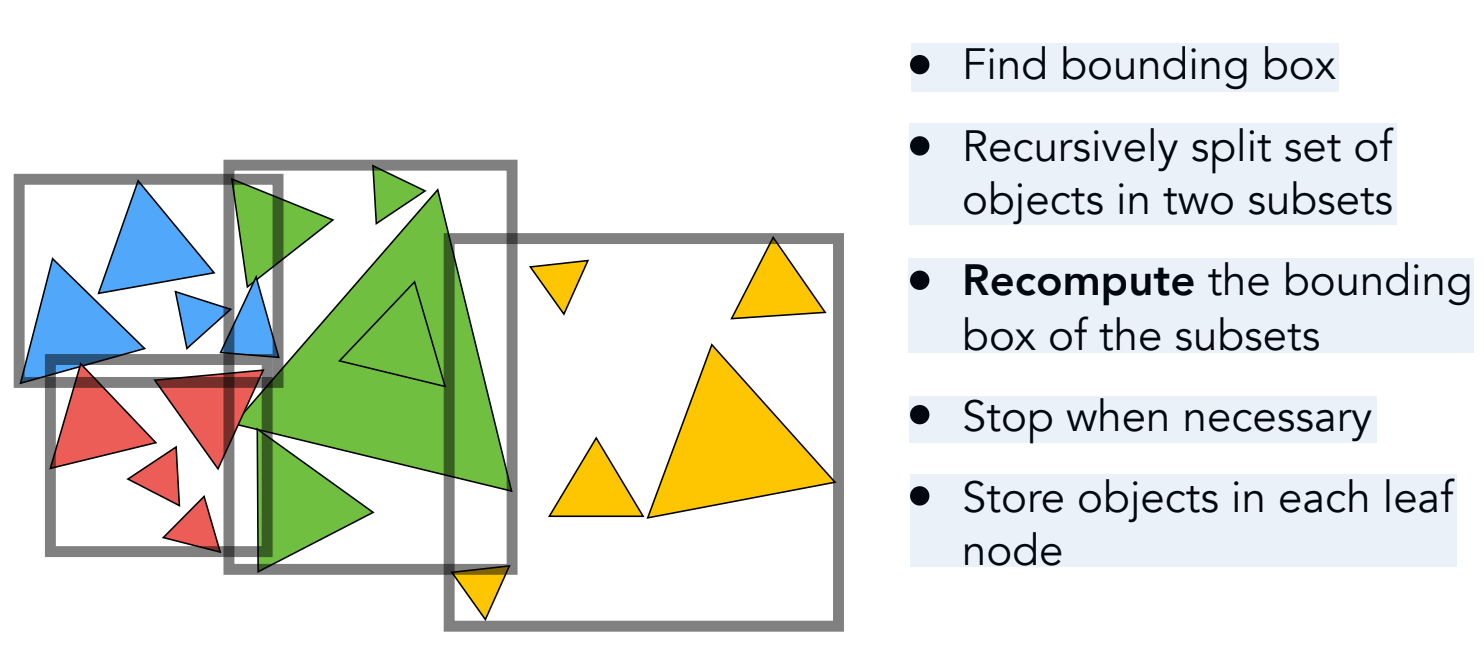
3.2 BVH 构建算法

递归构建流程

def build_bvh(objects, max_leaf_size=5):
    """
    递归构建 BVH

    Args:
        objects: 物体列表
        max_leaf_size: 叶子节点最大物体数量

    Returns:
        BVHNode: BVH 树的根节点
    """
    node = BVHNode()

    # 1. 计算包围所有物体的 AABB
    node.bbox = compute_bounding_box(objects)

    # 2. 停止条件：物体数量足够少
    if len(objects) <= max_leaf_size:
        node.objects = objects
        return node

    # 3. 选择分割轴和分割点
    axis, split_pos = choose_split(objects)

    # 4. 将物体分成两组
    left_objects = [obj for obj in objects if obj.centroid[axis] < split_pos]
    right_objects = [obj for obj in objects if obj.centroid[axis] >= split_pos]

    # 5. 递归构建左右子树
    node.left = build_bvh(left_objects, max_leaf_size)
    node.right = build_bvh(right_objects, max_leaf_size)

    return node

分割策略

1. SAH (Surface Area Heuristic) - 表面积启发式

SAH 是最常用的分割策略，其核心思想是：

$$ \text{Cost} = C_{\text{trav}} + \frac{S_L}{S_P} \cdot N_L \cdot C_{\text{isect}} + \frac{S_R}{S_P} \cdot N_R \cdot C_{\text{isect}} $$

其中：

$C_{\text{trav}}$：遍历节点的代价
$S_P, S_L, S_R$：父节点、左子节点、右子节点的表面积
$N_L, N_R$：左右子节点包含的物体数量
$C_{\text{isect}}$：求交测试的代价

物理意义：包围盒表面积越大，光线击中的概率越高。

2. 中位数分割

更简单但次优的方法：

选择物体重心跨度最大的轴
按该轴坐标排序，从中位数处分割

def choose_split_median(objects):
    """中位数分割策略"""
    # 计算每个轴的跨度
    centroids = [obj.centroid for obj in objects]
    extents = [max(c[i] for c in centroids) - min(c[i] for c in centroids)
               for i in range(3)]

    # 选择跨度最大的轴
    axis = extents.index(max(extents))

    # 按该轴排序，取中位数
    sorted_objects = sorted(objects, key=lambda obj: obj.centroid[axis])
    split_pos = sorted_objects[len(objects) // 2].centroid[axis]

    return axis, split_pos

3.3 光线遍历算法

BVH 的遍历是一个递归过程，采用深度优先搜索：

def intersect_bvh(ray, node, t_min=0.0, t_max=float('inf')):
    """
    光线与 BVH 求交

    Returns:
        hit_record: 最近的交点信息，若无交点则返回 None
    """
    # 1. 包围盒测试：光线是否击中该节点的包围盒
    if not ray_box_intersect(ray, node.bbox, t_min, t_max):
        return None

    # 2. 叶子节点：与其中所有物体求交
    if node.is_leaf():
        closest_hit = None
        closest_t = t_max

        for obj in node.objects:
            hit = ray_object_intersect(ray, obj)
            if hit and t_min < hit.t < closest_t:
                closest_hit = hit
                closest_t = hit.t

        return closest_hit

    # 3. 内部节点：递归遍历左右子树
    hit_left = intersect_bvh(ray, node.left, t_min, t_max)
    hit_right = intersect_bvh(ray, node.right, t_min, t_max)

    # 4. 返回最近的交点
    if hit_left and hit_right:
        return hit_left if hit_left.t < hit_right.t else hit_right
    elif hit_left:
        return hit_left
    else:
        return hit_right

优化技巧：

提前终止：找到左子树交点后，可以用该距离更新 t_max，提前剪枝右子树
排序遍历：优先访问距离光线起点更近的子节点

3.4 光线-AABB 求交算法

BVH 的高效依赖于快速的包围盒求交测试：

def ray_box_intersect(ray, bbox, t_min, t_max):
    """
    光线与 AABB 求交（Slab 方法）

    Args:
        ray: 光线 (origin, direction)
        bbox: 包围盒 (min_point, max_point)
        t_min, t_max: 有效距离范围

    Returns:
        bool: 是否相交
    """
    for axis in range(3):
        # 计算光线进入/离开该轴的 slab 的时间
        inv_d = 1.0 / ray.direction[axis]
        t0 = (bbox.min[axis] - ray.origin[axis]) * inv_d
        t1 = (bbox.max[axis] - ray.origin[axis]) * inv_d

        # 处理负方向
        if inv_d < 0:
            t0, t1 = t1, t0

        # 更新有效区间
        t_min = max(t_min, t0)
        t_max = min(t_max, t1)

        # 无交集
        if t_max < t_min:
            return False

    return True

Slab 方法原理：

AABB 可以看作三对垂直于坐标轴的平面（slabs）的交集。光线与盒子相交，当且仅当它与所有三对平面的交集非空。

3.5 BVH 的优势与代价

优势：

无重复存储：每个物体仅存储一次，内存效率高
构建速度快：O(N log N)，远快于 KD-Tree 的 O(N log² N)
动态场景友好：物体移动时只需更新包围盒，无需重建整棵树
硬件加速支持：现代 GPU（RTX 系列）直接在硬件层面支持 BVH

代价：

包围盒重叠：兄弟节点的包围盒可能重叠，导致光线需要同时遍历两个子树
包围盒冗余：物体分布稀疏时，包围盒可能包含大量空白空间

实际表现：

对于典型场景，BVH 比朴素求交快 100-1000 倍
渲染 1000 万三角形的场景，从数天降低到数秒

四、三种加速结构对比总结

4.1 综合对比表

维度	均匀网格	KD-Tree	BVH
划分方式	固定尺寸网格	自适应空间二分	物体层次分组
时间复杂度（构建）	O(N)	O(N log² N)	O(N log N)
时间复杂度（查询）	O(N) 最坏	O(log N) 平均	O(log N) 平均
空间复杂度	O(N + 网格数)	O(N × 重复因子)	O(N)
物体重复存储	是	是（严重）	否
包围盒重叠	否	否	是（可接受）
适用场景	均匀分布场景	空间静态、物体简单	通用场景
动态场景支持	差	差（需重建）	好（局部更新）
硬件加速	无	无	RTX GPU 原生支持
工业应用	体素渲染、粒子系统	早期学术研究	主流渲染器首选

4.2 选择建议

使用均匀网格：

物体均匀分布（如体素化医学数据、流体模拟）
场景尺寸已知且物体密度恒定
实现简单优先

使用 KD-Tree：

目前几乎不推荐用于光线追踪
仅在某些点云搜索、最近邻查询场景下使用

使用 BVH（推荐）：

三角网格模型渲染
复杂场景（物体分布不均）
动态场景（变形、动画）
需要硬件加速（GPU）
生产环境渲染器

4.3 现代渲染器的实际选择

电影级渲染器：

Pixar RenderMan: BVH
Arnold Renderer: BVH
V-Ray: BVH
Cycles (Blender): BVH

实时光线追踪：

NVIDIA OptiX: BVH（硬件加速）
DirectX Raytracing (DXR): BVH
Vulkan Ray Tracing: BVH

结论：对于初学者和实际应用，深入理解 BVH 的构建和遍历是最重要的，因为它是现代光线追踪的绝对基石。

五、实践：简易 BVH 实现

下面是一个简化的 BVH 实现示例，帮助理解核心概念：

from dataclasses import dataclass
from typing import List, Optional
import math

@dataclass
class AABB:
    """轴对齐包围盒"""
    min: Vec3
    max: Vec3

    def union(self, other: 'AABB') -> 'AABB':
        """合并两个包围盒"""
        return AABB(
            min=Vec3(
                min(self.min.x, other.min.x),
                min(self.min.y, other.min.y),
                min(self.min.z, other.min.z)
            ),
            max=Vec3(
                max(self.max.x, other.max.x),
                max(self.max.y, other.max.y),
                max(self.max.z, other.max.z)
            )
        )

    def surface_area(self) -> float:
        """计算表面积"""
        d = self.max - self.min
        return 2.0 * (d.x * d.y + d.y * d.z + d.z * d.x)

class BVHNode:
    """BVH 节点"""
    def __init__(self):
        self.bbox: Optional[AABB] = None
        self.left: Optional[BVHNode] = None
        self.right: Optional[BVHNode] = None
        self.objects: List = []

    def is_leaf(self) -> bool:
        return len(self.objects) > 0

def build_bvh(objects: List, max_leaf_size=4) -> BVHNode:
    """构建 BVH"""
    node = BVHNode()

    # 计算包围盒
    node.bbox = objects[0].bbox
    for obj in objects[1:]:
        node.bbox = node.bbox.union(obj.bbox)

    # 叶子节点
    if len(objects) <= max_leaf_size:
        node.objects = objects
        return node

    # 选择分割轴（最长轴）
    extents = node.bbox.max - node.bbox.min
    axis = 0 if extents.x > extents.y and extents.x > extents.z else \
           1 if extents.y > extents.z else 2

    # 按重心排序
    objects.sort(key=lambda obj: obj.centroid()[axis])
    mid = len(objects) // 2

    # 递归构建
    node.left = build_bvh(objects[:mid], max_leaf_size)
    node.right = build_bvh(objects[mid:], max_leaf_size)

    return node

def intersect_bvh(ray, node, t_min=0.0, t_max=float('inf')):
    """光线与 BVH 求交"""
    # 包围盒测试
    if not ray_box_intersect(ray, node.bbox, t_min, t_max):
        return None

    # 叶子节点
    if node.is_leaf():
        closest_hit = None
        for obj in node.objects:
            hit = obj.intersect(ray, t_min, t_max)
            if hit:
                closest_hit = hit
                t_max = hit.t  # 提前剪枝

        return closest_hit

    # 递归遍历
    hit_left = intersect_bvh(ray, node.left, t_min, t_max)
    if hit_left:
        t_max = hit_left.t

    hit_right = intersect_bvh(ray, node.right, t_min, t_max)

    return hit_right if hit_right else hit_left

参考资料

GAMES101: 现代计算机图形学入门 - 闫令琪 Lecture 14
TinyRaytracer - Dmitry V. Sokolov
Physically Based Rendering - Matt Pharr et al.
NVIDIA OptiX Programming Guide - BVH 硬件加速
Wald, I. (2007). “On fast Construction of SAH-based Bounding Volume Hierarchies”